アルゴリズム1
こんにちは、kazutoです。今回からアルゴリズムについて扱っていきます。まずは、基本的な探索方法について実際にプログラムを組んで解説していきます。
アルゴリズム
まずは、アルゴリズムは、どのような物なのかをポイントを抑えていきましょう。
- アルゴリズムとは
- フローチャートを読み解こう
- アルゴリズム基本構造
アルゴリズムとは
アルゴリズムとは、問題を解決するための方法や手順のことを指します。要するに問題を解決するための実行手順みたいなものです。コンピューターは、プログラムに書かれた手順の通り動作をします。この「どのように処理させるか」という手順の事をアルゴリズムと呼びます。アルゴリズムは、必ずしも、コンピュータの世界だけで使われているわけではなく、色々な場面で使われています。
一般の例だと
- 料理のレシピ
- カーナビや乗り換え案内
- Googleの検索アルゴリズム
などが上がると思います。
フローチャートを読み解こう
アルゴリズム(手順)を可視化をするためにフローチャートという方法が用いられます。フローチャートとは、処理の流れを表す図になります。
フローチャートでは下記の様な記号を使って処理の流れを表します。
| 記号 | 概要 |
|---|---|
 |
処理の開始と終了を表す |
 |
処理を表す |
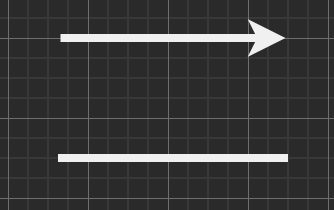 |
処理の流れを表す。処理の流れる方向が、上から下、左から右という原則から外れる場合は矢印を用いて明示する |
 |
条件によって流れが分岐する判定処理を表す |
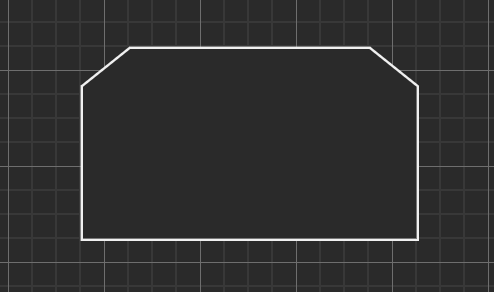 |
繰り返し処理の開始を表す |
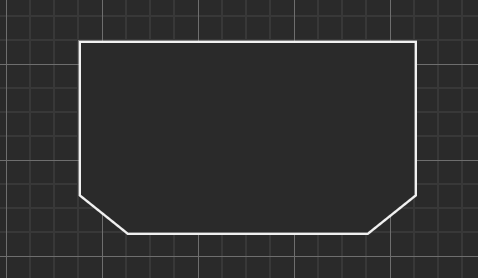 |
繰り返し処理の終了を表す |
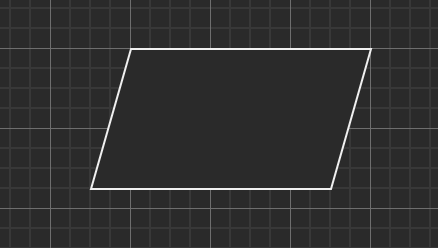 |
データを表す |
最初は慣れないと思いますが、実際にフローチャートにして処理の流れを可視化した方がスムーズにコーディングができると思います。
アルゴリズム基本構造
プログラミングは、
- 順次構造
- 選択構造
- 繰り返し構造
と上記3つの基本構造を組み合わす事で、基本的な処理から複雑な処理まで表現できる様になっています。
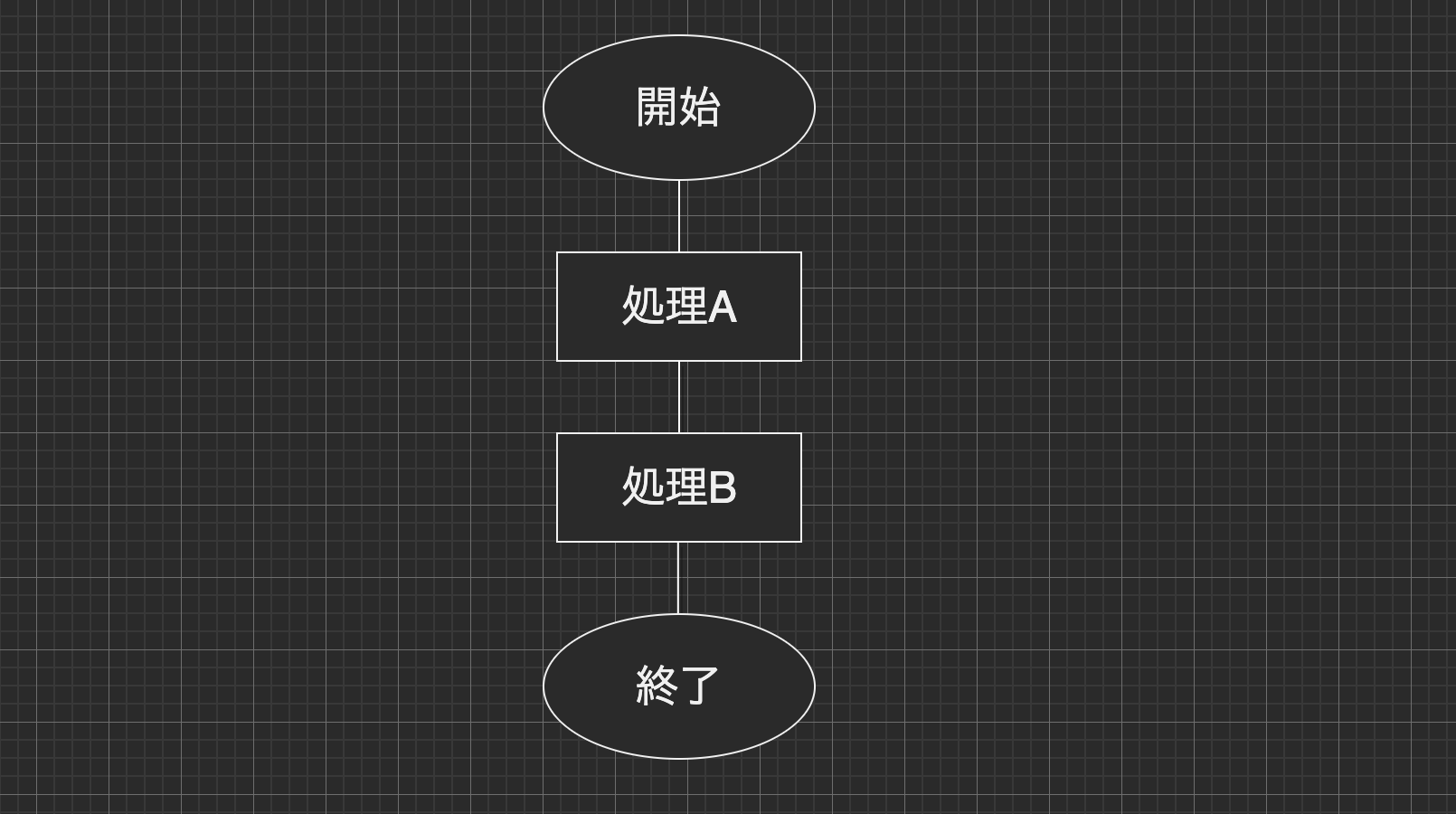
順次構造とは、処理する順番に記述されているプログラムの構造の事を指します。フローチャート では下記の様に表現できます。
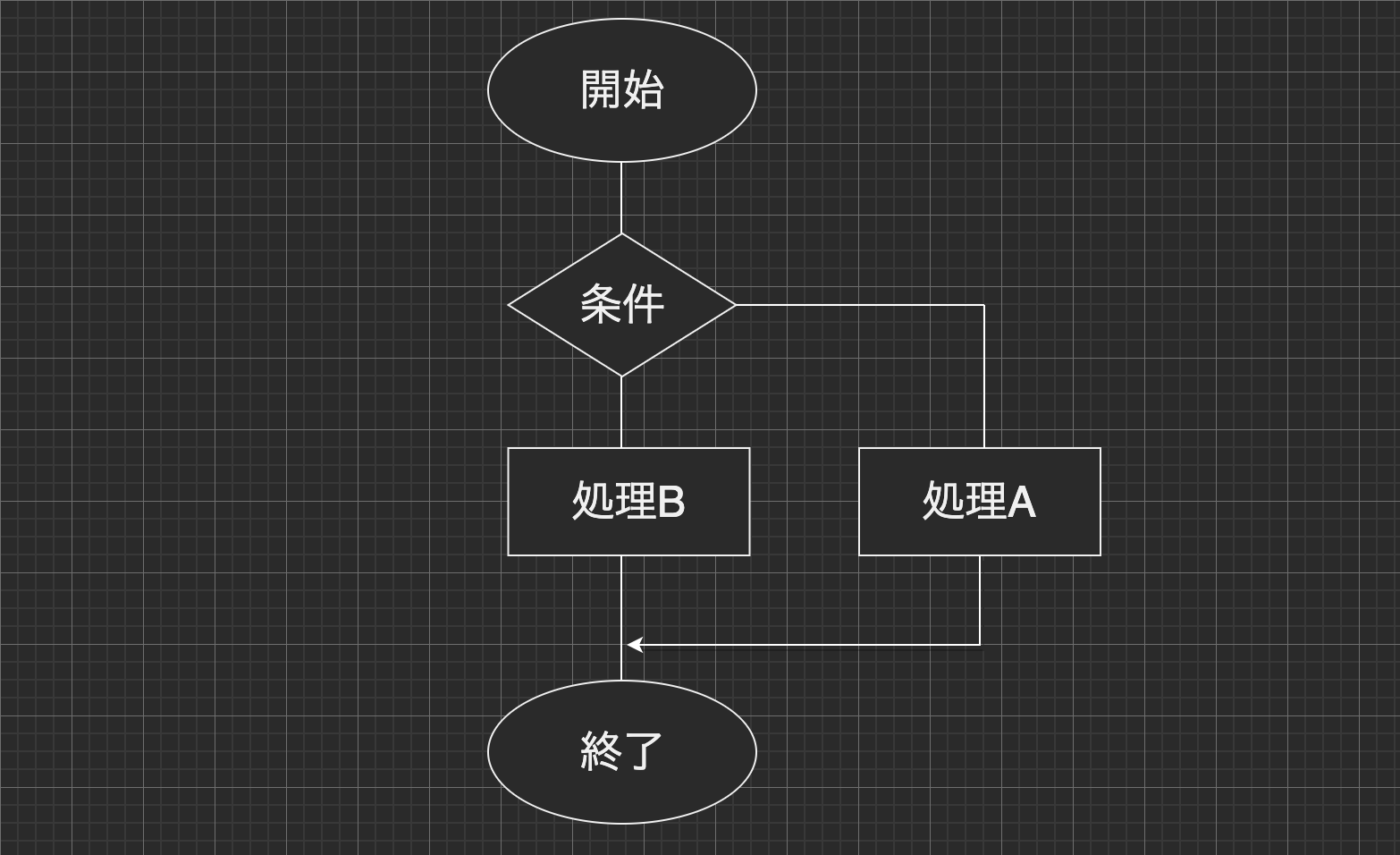
選択構造とは、条件を判断をし、次に実行する処理が分岐する構造の事を指します。フローチャート では下記の様に表現できます。
繰り返し構造とは、条件が満たされるまで間、または条件が満たされるまで、同じ処理を繰り返す構造の事を指します。なお、繰り返し構造には2種類のパターンがあります。
- 前判定型
- 後判定型
です。
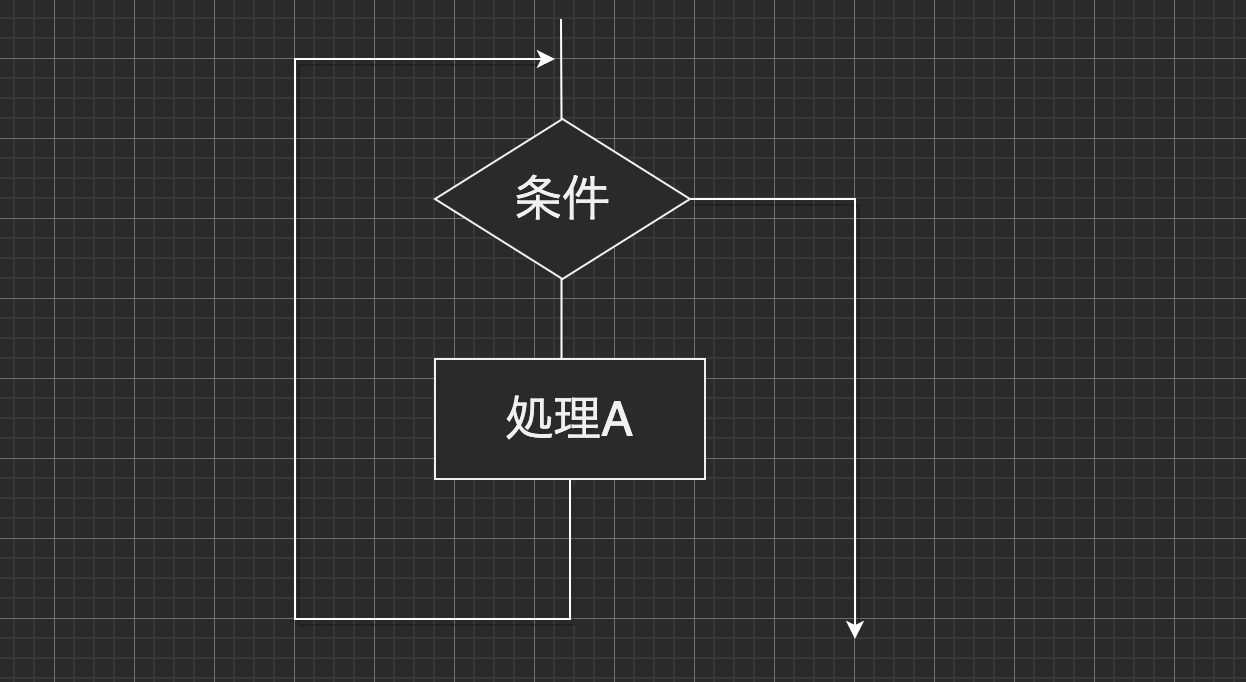
先に条件を判断して処理を繰り返すかどうか決める場合を前判定型といいます。フローチャート では下記の様に表現できます。
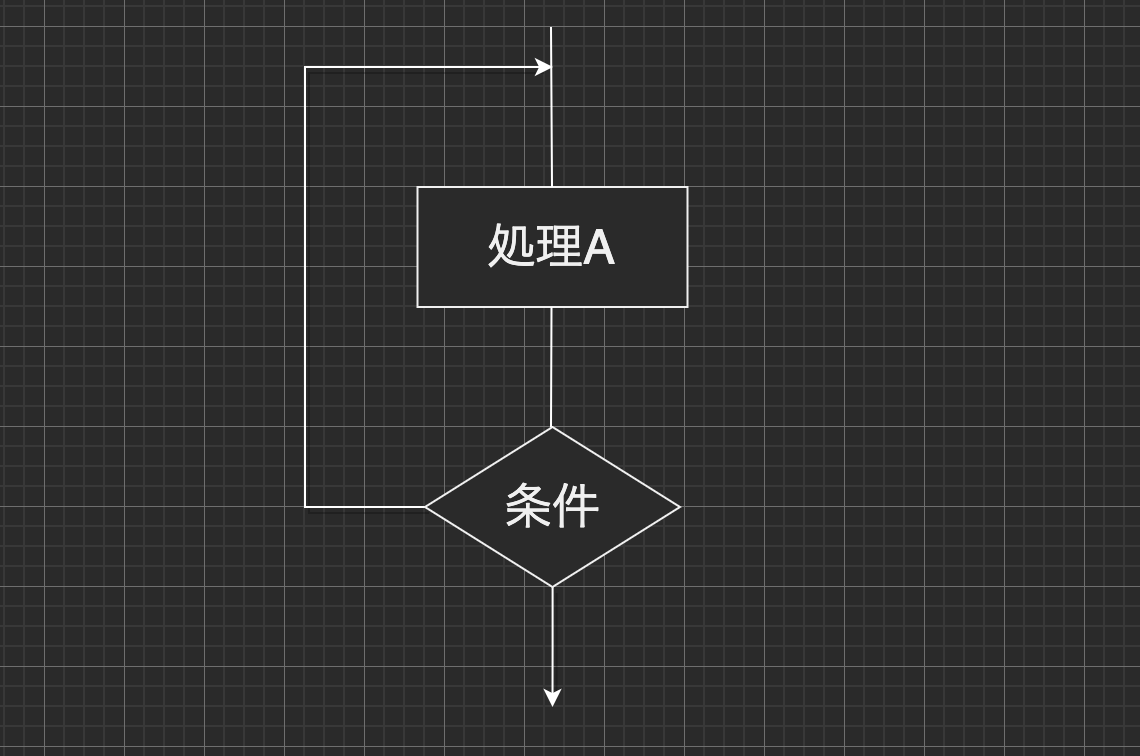
処理した後で、条件を判断して繰り返すかどうか決める場合を後判定型といいます。フローチャート では下記の様に表現できます。
次のトピックから上記の3つのアルゴリズム構造を用いて、2つの探索アルゴリズムをコーディングをしていきましょう。
※探索アルゴリズムとは
探索アルゴリズムとは、配列など複数ある箱から目的なデータを探し出すアルゴリズムの事を指します。
線形探索法
まず初めに線形探索法について解説していきます。線形探索法とは、該当するデータが一致するまで先頭から順番に探すアルゴリズムの事を指します。文字だけでは、理解できないと思うので、下記の動画を参照してください。
フローチャート を確認をしよう
線形探索法の特徴を抑えた所で、線形探索法をフローチャートで表現をしていきましょう。
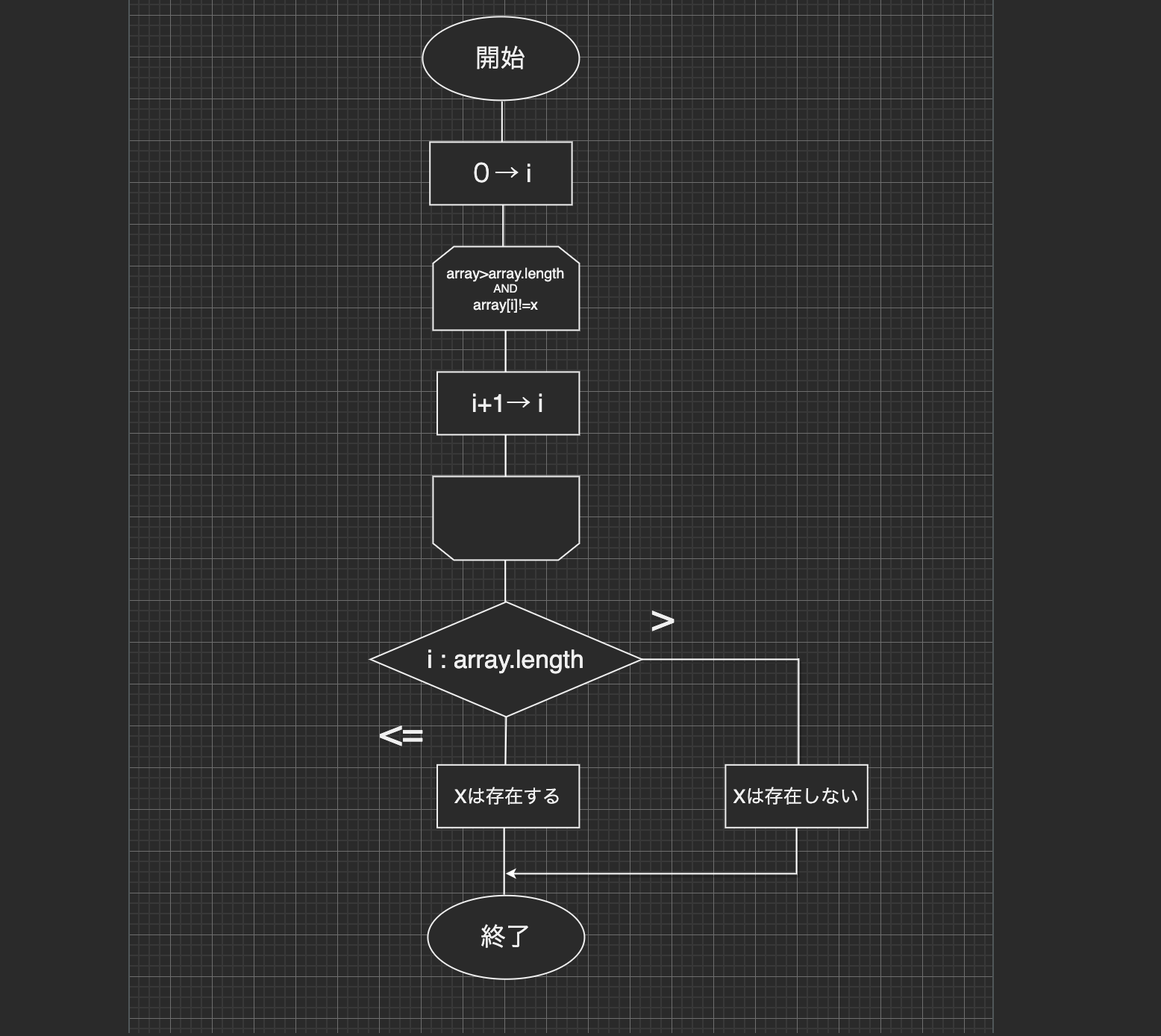
線形探索はフロチャートで表すと上記の様になります。シンプルにプログラムを組めそうですね。上記のフローチャートを参考に次のトピックで、実際にソースコードに置き換えてみましょう。
コードに置き換えよう
フローチャート を確認をした所で、実際にソースコードに置き換えていきましょう。
| 変数 | 概要 |
|---|---|
| array | 配列 |
| x | 検索対象 |
| i | 添字 |
def linear_search(array,x)
i = 0
while i < array.length && array[i] != x
i+=1
end
puts i < array.length ?
"#{x}は配列の#{i}番目に格納されています。"
:
"#{x}は見つかりませんでした"
end
linear_search([2,13,1,4],13)
それでは、解説していきます。
i = 0まずは、変数iを初期化をします。
while i < array.length && array[i] != x
i+=1
end上記のソースコード(while)で実際に配列の中を探索をしています。条件分岐の内容は、変数iが配列の長さより値が小さいかつ配列の中にxが見つからない限りループ処理を繰り返すとなります。
puts i < array.length ?
"#{x}は配列の#{i}番目に格納されています。"
:
"#{x}は見つかりませんでした"最後にxの有無を出力をします。xが配列の中に見つかったというシチュエーションを想像をして見てください。xが配列内に見つかるという事は、配列の長さ内で処理が完結している事がわかります。つまり、i < array.length の関係が成り立っている場合は、xが見つかったという事になります。したがって、上記の様な三項演算子を用いた分岐の形になりました。
以上で、線形探索の解説を終了します。線形探索は、アルゴリズムの中でも簡単にコード化できます。また、フローチャート を用いて実装する前に、アウトラインを整えるだけでもコーディングしやすくなるのでおすすめです。
二分探索
最後に二分探索について解説していきます。二分探索法とは、データの集合をざっくり2つに分けて対象を絞り込んでいく探索方法です。なお前提として、対象のデータの集まりがソート済みで規則性が持つ場合のみ有効な、探索アルゴリズムです。文字だけでは、理解できないと思うので、下記の動画を参照してください。
フローチャート を確認をしよう
二分探索の特徴を押さえた所で、二分探索をフローチャートで表現をしていきます。
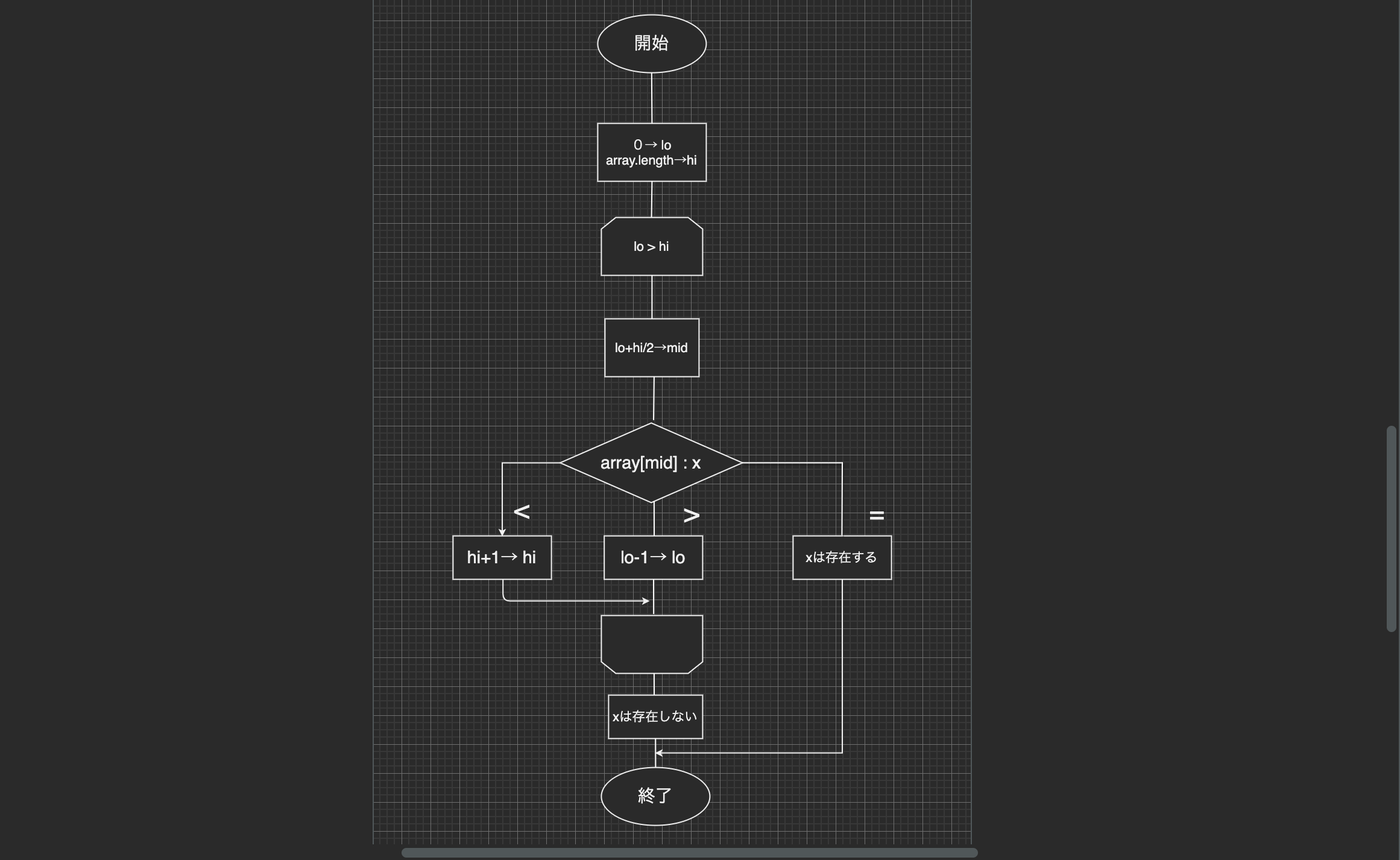
二分探索はフロチャートで表すと上記の様になります。線形探索を比較すると少し複雑ですね。上記のフローチャートを参考に次のトピックで、実際にソースコードに置き換えてみましょう。
コードに置き換えよう
フローチャート 確認をした所で、実際にソースコードに置き換えていきましょう。
| 変数 | 概要 |
|---|---|
| array | 配列 |
| x | 探索対象 |
| hi | 添字の上限値 |
| lo | 添字の下限値 |
| mid | 添字の中央値 |
def binary_search(array,x)
lo = 0
hi = array.length
while lo < hi
mid = (lo+hi)/2
if array[mid] == x
return puts "#{x}は配列の#{mid}番目にあります。"
elsif array[mid] > x
hi-=1
elsif array[mid] < x
lo+=1
end
end
puts "#{x}は見つかりませんでした" if array[mid] != x
end
binary_search([1,2,3,4,6,7,8,9],0)
では解説していきます。
lo = 0
hi = array.lengthまず初めに
- 添字の下限値(lo)
- 添字の上限値(hi)
を初期化します。
while文での繰り返し処理が始まる前に上限値と下限値を求め、中央値を求める準備を行います。
while lo < hi
mid = (lo+hi)/2
if array[mid] == x
return puts "#{x}は配列の#{mid}番目にあります。"
elsif array[mid] > x
hi-=1
elsif array[mid] < x
lo+=1
end
end繰り返し処理の条件を言語化すると下限値より上限値の値が大きい限りループ処理を繰り返すとなります。一見、上記の条件だと無限ループに陥りそうですが、心配ありません。xが見つかる分岐処理以外の場合は、上限値または下限値の値を引いたり、足したりするので、lo < hiという条件式は成り立ち、無限ループには、陥りません。
mid = (lo+hi)/2上記のソースコードで中央値を求めています。上限値と下限値の合計を求め、その範囲を2で割った数が、中央値になります。
if array[mid] == x
return puts "#{x}は配列の#{mid}番目にあります。"
elsif array[mid] > x
hi-=1
elsif array[mid] < x
lo+=1
end上記のソースコードで条件分岐を行っていきます。
if array[mid] == x
return puts "#{x}は配列の#{mid}番目にあります。"探索対象であるxが見つかったら、xが配列の何番目にあったのかを出力をし、強制終了をします。
elsif array[mid] > x
hi-=1探索対象xが、現在の配列の値よりも小さい場合は、上限値(hi)に1を引き、範囲を左に狭めます。なお、xが見つからない場合は、上限値の値が下限値の値より低くなった段階でループ処理が止まります。
elsif array[mid] < x
lo+=1探索対象xが、現在の配列の値よりも大きい場合は、下限値(lo)に1を足し、範囲を右に狭めます。なお、xが見つからない場合は、下限値の値が上限値の値より大きくなった段階でループ処理が止まります。
puts "#{x}は見つかりませんでした" if array[mid] != x処理の最後に探索対象xが見つからない場合にはxが見つからない事を出力します。
以上で、「アルゴリズム1」が終了になります。
まとめ:アルゴリズム1
今回は、アルゴリズムの概要と探索について解説していきました。具体的な探索方法として
- 線形探索
- 二分探索
がありました。探索アルゴリズムは他のアルゴリズムと比べ、とてもシンプルで構造を捉えやすいです。まずは、探索アルゴリズムでアルゴリズムに慣れ、他のアルゴリズムにも対応できる様になっていきましょう。
以上、kazutoでした。
